 Aktuelle Koordinationschemie (AC7–9)
Aktuelle Koordinationschemie (AC7–9) Aktuelle Koordinationschemie (AC7–9)
Aktuelle Koordinationschemie (AC7–9)2 SWS,
Fr 11–13, online via Zoom
Beginn: 6. November 2020, Ende: 12. Februar 2021
Die Vorlesung wird als Online-Kurs angeboten, Sie benötigen daher für die Teilnahme einen Computer mit Lautsprechern und einen Internetanschluss. Um teilzunehmen, melden Sie sich bitte im LSF an. Hierdurch bekomme ich Zugang zu Ihrer Email-Adresse. Vor der ersten Vorlesung erhalten Sie über Email einen Link, der Ihnen zur Vorlesungszeit die Teilnahme freischaltet.
Ich benutze Zoom, wobei Sie mich hören, ich Sie aber zu Beginn stummschalte und auch Ihr Video abschalte. Während der Vorlesung sehen Sie Graphiken, Formeln, etc. in einer pdf-Datei. Während ich dazu etwas erzähle, scrolle ich durch den pdf und bringe das, was ich sonst an die Tafel geschrieben hätte, als Notiz an. Einzelheiten, wie Sie Zugang zu den Dateien erhalten, erfahren Sie in der ersten Vorlesungsstunde. Drucken Sie bitte nicht den nachfolgenden Text aus. Der Lehrinhalt wird ein erneuerter sein. Ich lasse das bisherige Skript nur im Netz, damit Sie immerhin einen Eindruck von den Dingen erhalten, um die es gehen soll.
Die Vorlesungszeit ist zweimal 45 Minuten, wir machen also von 12:00 bis 12:15 eine Pause. Während dieser Pause läuft die Schaltung einfach weiter, so dass Sie dann die Chatfunktion benutzen können, um Fragen zu stellen. Diese Fragen versuche ich sofort zu beantworten. Die zweite Möglichkeit ist von 13:00 bis 13:15 nach dem Ende der Vorlesung; ich lasse die Verbindung dann noch für eine Viertelstunde für Chats offen, die beim folgenden Termin angesprochen werden. Wenn danach etwas ist: wie immer per Email.
Beachten Sie für alle Fragen rund um das Speichern und Weiterverbreiten der präsentierten Inhalte einen rechtlichen Hinweis.
Die Klausur für das WS 2020/2021 findet am Donnerstag, dem 18. März 2021, von 10:15–11:45 Uhr im Baeyer-HS statt. Melden Sie sich bitte auf der CUP-Webseite an.
Alte Klausuren:
| WS 2016/2017: | Klausur | Lösung |
| WS 2015/2016: | Klausur | Lösung |
| WS 2014/2015: | Klausur | Lösung |
| Klausur | Lösung | |
| WS 2013/2014: | Klausur | Lösung |
| Klausur | Lösung | |
| WS 2012/2013: | Klausur | Lösung |
| Klausur | Lösung | |
| WS 2011/2012: | Klausur | Lösung |
| Klausur | Lösung | |
| WS 2010/2011: | Klausur | Lösung |
| Klausur | Lösung | |
| WS 2009/2010: | Klausur | Lösung |
| Klausur | Lösung | |
| WS 2005/2006: | Klausur | Lösung |
| WS 2004/2005: | Klausur | Lösung |
Master-Studiengang Chemie: AC 7, 8 oder 9
Der Vorlesung Koordinationschemie II vertieft den Stoff der Vorlesung Einführung in die Koordinationschemie in verschiedene Richtungen. Ziel ist es, unter besonderer Berücksichtigung der verwendeten Methoden aktuelle Schwerpunkte der Koordinationschemie anzusprechen.
Die aktuelle Koordinationschemie profitiert als sehr methodenreiche Disziplin vom enormen Fortschritt der technischen Möglichkeiten. Gerade bei den hier interessierenden Methoden wie der Strukturaufklärung an Kristallen, den verschiedenen spektroskopischen Verfahren und, als verbindende Klammer, der Computerchemie – hier vor allem die DFT-Methoden an offenschaligen Spezies – hat es in der jüngeren Vergangenheit beachtliche Fortschritte gegeben. Dabei haben diese Methoden ihren Weg aus den spezialisierten Arbeitskreisen in die experimentell-synthetische Laborpraxis gefunden. Ziel der Vorlesung ist es, genau solche Methoden und Konzepte vorzustellen, die heute zur Arbeit einer synthetisch orientierten Gruppe zum Standard gehören, … und daher Teil praktisch jeder koordinationschemischen Publikation sind.
Ausgangspunkt ist die Vorlesung Koordinationschemie des Bachelorstudienganges (AC 3). Die dort formulierten Konzepte sind so ausgewählt, dass Ihnen dort kein zu stark vereinfachtes Scheinwissen vermittelt wurde, sondern, im Gegenteil, solche Modellvorstellungen eingeführt wurden, die sich ohne Abstriche erweitern lassen.
Das soll nun in dieser Vorlesung geschehen und zwar in aktualisierter Form. Aus den vergangenen Semestern wird zunächst das Methodenkapitel übernommen. Dort fehlte bislang die UV-vis-Spektroskopie, was in diesem Semester nachgeholt werden soll, ein weiterer Schwerpunkt werden p-Block-Komplexe sein.
Wir beginnen daher mit den folgenden Themen: (1) Methoden (wie bisher), (2) p-Block-Komplexe, (3) d-Orbitale, (4) UV-vis-Spektren, Aufnahme und Interpretation. Das Skript für das erste Kapitel können Sie auch in einer pdf-Version herunterladen. Später werden einige Inhalte hinzukommen, bei denen mir der Urheberschutz wichtig ist. Diese ergänzte pdf-Datei finden Sie dann in einer passwortgeschützten Datei.
Computerchemische Rechnungen sind entweder mit Gaussian ausgeführt, das Sie auf den Rechnern in den WAP-Räumen in der Version 16 vorfinden. Die Ergebnisse können sie mit GaussView ansehen, das Sie ebenfalls dort vorfinden. Frei verfügbar ist Orca, zu dessen Bedienung einschließlich der Darstellung der Ergebnisse Sie ebenfalls auf freie Programme zugreifen können. Empfehlenswert sind zum Beispiel Gabedit oder Avogadro.
Prüfen Sie hier, ob Ihr Browser das Skript korrekt darstellt.
Die erste Lehreinheit knüpft an den Inhalt der Lehreinheit 2 der Einführung in die Koordinationschemie an. Es geht um die Frage, wie ein Komplexgleichgewicht in wässriger Lösung analysiert werden kann. Im Mittelpunkt steht als wohlvertrauter Ligand Tartrat, und zwar das C2-symmetrische l-Tartrat, das in mehr oder weniger alkalischer Lösung eingesetzt wird. Um übersichtlich zu bleiben, wird ein Palladium(II)-Zentrum mit eingeschränkter Funktionalität eingesetzt: zwei der vier (warum vier?) Bindungsstellen des Zentralmetalls sind durch einen zweizähnigen Stickstoff-Chelatliganden blockiert. Bei der Umsetzung des Edukts [(R,R-chxn)PdII(OH)2] (chxn = 1,2-Diaminocyclohexan) mit Weinsäure (H2tart) in wässrig-alkalischer Lösung entstehen neue Komplexverbindungen. Da diese diamagnetisch sind (warum?), können 13C-NMR-Spektren mit Standardmethoden ausgewertet werden (1H-NMR-Spektren helfen nicht viel weiter; warum nicht?).
13C-NMR Spektren in D2O bei verschiedenen molaren Verhältnissen [(R,R-chxn)Pd(OH)2]:l-H2tart:OH− von 1:1:1, 3:1:0, 1:1:2 und 3:1:2. Die auf der Abszisse angegebene chemische Verschiebung bezieht sich auf TMS (δ = 0 ppm). Spektrum a: Dinatrium-l-tartrat in D2O; Komplexspezies sind farbig dargestellt:
Die Spektren werden auf folgende Aspekte hin untersucht:
• Welche Komplexspezies entstehen?
• Wodurch wird gesteuert, welche Spezies dominiert?
Die wichtigste und zur nächsten Lehreinheit überleitende Frage ergibt sich jedoch aus der Betrachtung der Spektren d und e: Wie ist es zu verstehen, dass ein Gleichgewicht wie
L2Pd2(tartH−2) + 2 OH− = LPd(tartH−2) + LPd(OH)2
nach dem 13C-NMR-Spektrum praktisch vollständig auf der rechten Seite liegt, dass also der hoch eingeschätzte Chelateffekt Schwächen zeigt (L = R,R-chxn)? Die oft als chaotisch empfundene Chemie in wässriger Lösung zeigt hier eine wesentliche Besonderheit: die erwarteten Komplexgleichgewichte spielen mit Protolysegleichgewichten zusammen. Liegt, wie im Beispiel, auf der einen Seite des Gleichgewichts starke Säure oder Base frei vor, so gewinnt die Natur bei der Verschiebung des Gleichgewichtes auf die andere Seite Neutralisationsenthalpie. Dieser Beitrag kann entscheidend sein, wenn die Komplexstabilität nicht sehr hoch ist – so wie hier: beachten Sie die großen Mengen an freiem Ligand zum Beispiel in Spektrum b.
Preetz et al. berichten über die Synthese und Charakterisierung gemischter Chlorido-fluorido-platinate(IV) der allgemeinen Formel [PtFnCl6 − n]2− für n = 0–6. Wieviele Komplexspezies erwarten Sie? Beachten Sie bei den folgenden Überlegungen, dass der I=½-Kern 195Pt eine natürliche Häufigkeit von ca. 34% hat, während Fluor ein Reinelement ist; auch hier ist I = ½. Im 195Pt-NMR-Spektrum sind die Signale aller Spezies gut aufgelöst und nicht überlagert. Eine der Spezies ergibt das folgende Multiplett (ohne Berücksichtigung von 35Cl-Satelliten):
Welche? (Quelle: E. Parzich, G. Peters, W. Preetz, Z. Naturforsch. B 1993, 48, 1169–1174.) Welches 19F-Spektrum erwarten Sie, wenn Sie von einer 19F-19F-Kopplung ausgehen, die merklich kleiner als die 195Pt-19F-Kopplung ist (vernachlässigen Sie auch hier Chlor-Satelliten)?
Die Verkürzung der Relaxationszeiten in der Umgebung eines paramagnetischen Teilchens führt dazu, dass die Signale NMR-aktiver Kerne innerhalb eines charakterischen Radius' im Untergrundrauschen verschwinden. Der Radius dieser verblindeten Region um ein paramagnetisches Atom hängt vom paramagnetischen Element und dessen Spinzustand ab, außerdem von der Art des NMR-Kerns. Der Umstand, dass in Großteil der Literatur zur paramagnetischen NMR-Spektroskopie den Eisen(III)-Porphyrinen gewidmet ist, hängt mit dem ungewöhnlich geringen Radius des blinden Bereichs zusammen. Typisch ist dagegen zum Beispiel in der 13C-NMR-Spektroskopie, dass alle Spezies in einer ca.-10-Å-Umgebung um ein Zentralmetall herum im Spektrum keine Signale ergeben (ca. 15 Å in der 1H-NMR-Spektroskopie). Dies heißt, dass die Liganden eines paramagnetischen Komplexes üblicherweise nicht zu Signalen führen.
Trotz dieser Einschränkung gibt es eine Standardanwendung der Methode in der Koordinationschemie, nämlich die Evans-Methode. Hierbei wird die molare Suszeptibilität χm aus der Differenz der chemischen Verschiebungswerte einer nicht koordinierenden Substanz und der molaren Konzentration des Metallkomplexes errechnet:
| χm = | 3 Δ δ |
| cM |
Die meist interessierende Zahl der Bohrschen Magnetonen (deren Berechnung nach der Spin-only-Formel kam in der Koordinationschemie I vor), ergibt sich dann aus der Boltzmann-Konstante, der Temperatur, der Suszeptibilität, der Vakuumpermeabilität, der Avogadro-Konstante und dem Bohrschen Magneton:
| μeff2 = | 3 kB T χm |
| μ0 NA μB2 |
Die Röntgenstrukturanalyse an Einkristallen gilt als Methode, die wenig Interpretationsspielraum lässt: so, wie es herauskommt, so ist es halt. Dass trotz der hohen Aussagesicherheit der Röntgenstrukturanalyse allerhand Unsinn publiziert wird, zeigen die folgenden Beispiele. Das Lernziel ist, dass Sie zwei besonders verdächtige Fälle erkennen: wenn (1) die publizierten Daten selbst nicht konsistent sind, und wenn (2) das Ergebnis den Regeln der Koordinationschemie zuwiderläuft.
Übungsobjekte sind fünf Strukturanalysen an Komplexen mit dem Anion des Salicylaldehyds (saldH), das in der Literatur meist Salicylaldehydat oder Formylphenolat genannt wird, und einem zweiwertigen Zentralmetall. Die lösungsmittelfrei kristallisierenden Komplexe werden genauso formuliert wie ein schon länger bekannter Prototyp, die Kupfer(II)-Verbindung [CuII(sald)2], deren Ci-symmetrische Struktur (nicht C2h, da das Molekül nicht vollständig planar ist) zuletzt 1995 bestätigt wurde (A. Elmali, Y. Elerman, I. Svoboda, H. Fuess, Z. Kristallogr. NCS 1995, 210, 612). Die Atomabstände im Kupferkomplex zeigen eine kürzere Bindung zwischen dem Zentralmetall und dem Phenol-O-Atom (1.887 Å) und eine längere Bindung zwischen dem Kupferatom und dem Aldehyd-O-Atom (1.935 Å):
Alle neueren Arbeiten an homologen Verbindungen erschienen in Acta Crystallogr., Sect. E, was den Vorteil hat, dass die zugrundeliegenden Beugungsdaten mitpubliziert sind, man kann also alles nachrechnen. Im Einzelnen ist M:
| MII | Autoren | Jahr | Band | Artikel |
|---|---|---|---|---|
| Mn | Q. Wang, X.-N. Fang | 2006 | E62 | m1492 |
| Fe | Y.-M. Yang, P.-C. Lu, T.-T. Zhu, C.-H. Liu | 2007 | E63 | m1613 |
| Co | X.-Y. Qiu | 2006 | E62 | m1191 |
| Ni | Y.-G. Li, H.-J. Chen | 2006 | E62 | m1038 |
| Zn | Z.-Y. Xiong, L.-J. Liu | 2005 | E61 | m863 |
Wir diskutieren als Übung, wo jeweils das Problem sein könnte (Anmerkung: die hier diskutierten Strukturanalysen wurden inzwischen von Acta Crystallogr. zurückgezogen; in einigen Fällen dürfte es sich um bewusste Betrugsversuche handeln); siehe [actae_retraction_2010]. Als Grundlage verwenden wir den Zusammenhang zwischen Atomformfaktoren und Temperaturparametern:
Der abgebildete Zusammenhang wir auch unmittelbar beim Betrachten von Beugungsbildern deutlich:

Das Ergebnis einer Strukturanalyse stimmt – vor allem, wenn die intermolekularen Wechselwirkungen klein sind – innerhalb von typischerweise 2–3 pm (0.02–0.03 Å) mit routinemäßigen computerchemischen Rechnungen überein. Abweichungen sind umso größer, je weniger die im Computer behandelte Baueinheit und ihre Einbindung in die Umgebung mit der experimentell untersuchten Situation übereinstimmt.
Über eine Bestätigung der stabilsten Struktur hinaus bieten die Rechnungen (1) Gesamtenergien, auch von nicht experimentell gefundenen instabilen Isomeren einschließlich Übergangszuständen, (2) Orbitale und Orbitalenergien, und (3) weitere abgeleitete Größen wie UV/Vis-Absorptionen und NMR-Verschiebungen.
Schauen wir uns diese Aspekte im Beispiel an: Unter den im Röntgenkapitel als verdächtig erkannten Strukturanalysen war die eines quadratisch-planaren Zink-Salicylaldehyd-Komplexes, [Zn(sald)2], saldH = Salicylaldehyd. Die Strukturanalyse ergab ein Ci-symmetrisches Molekül mit den angegebenen Zn-O-Abständen:
Abstände in Å von Zn zu: Ophen 1.89, Oald 1.95.
Deckt sich dieses Ergebnis mit einer computerchemischen Analyse? Hierzu zuerst eine Referenzverbindung.
[Zn(sald)2(H2O)2] entsteht bei der Reaktion von Zinkacetat und der doppeltmolaren Menge Salicylaldehyd in Wasser:
Zn(OAc)2 + 2 saldH + 2 H2O → [Zn(sald)2(H2O)2] +2 HOAc
Die Röntgenstrukturanalyse an den farblosen Kristallen ergibt den Aufbau des Einkernkomplexes:
Mittlere Abstände in Å von Zn zu: Ophen 2.03, Oald 2.11, Oaq 2.09.
Die Rechnung (Gaussian- Eingabedatei und Ausgabedatei) ergibt mit der DFT-Hybridmethode B3LYP und dem kleinen Basissatz tzvp die folgende Struktur:
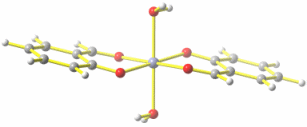
Abstände in Å von Zn zu: Ophen 2.00, Oald 2.12, Oaq 2.27.
Es wird deutlich, dass die Übereinstimmung der Atomabstände innerhalb der Chelatringe gut ist, dass aber der Abstand zum Aqualigand in der Rechnung erheblich abweicht. Wir diskutieren den Grund hierfür, der auch für den offensichtlichen Unterschied bei der Konformation verantwortlich ist (intermolekulare Wasserstoffbrückenbindungen im Kristall gegenüber [schwachen und in der Realität meist irrelevanten] intramolekularen Wasserstoffbrückenbindungen im isolierten Computer-Molekül).
Hierzu eine Übung. Verwenden Sie eine Orca-Eingabedatei, um den Zinkkomplex einmal mit (so wie es in der Datei vorgesehen ist) und einmal ohne Lösungsmittelkorrektur (Anweisung cpcm entfernen) zu optimieren.
Die B3LYP/tzvp-Rechnung an quadratisch-planarem [Zn(sald)2] führt zu den folgenden Parametern:
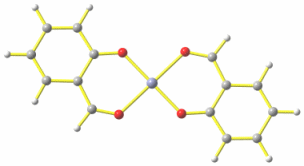
Abstände in Å von Zn zu: Ophen 1.92, Oald 2.08.
Für die recht großen Abweichungen zum Experiment lassen sich keine starken intermolekularen Wechselwirkungen verantwortlich machen. Ein stärkerer Hinweis, dass etwas nicht stimmt, wird durch die routinemäßige Behandlung des Rechenergebnisses gewonnen: der Strukturoptimierung folgt stets eine sogenannte Frequenzrechung, die zeigt, ob die zu einem Extremum führende kleinste-Fehlerquadrate-Verfeinerung der Strukturoptimierung ein Energieminimum oder ein Maximum, also einen Übergangszustand ergeben hat. Im letzteren Fall treten Schwingungen mit negativer Anregungsenergie auf, deren Auslenkung oft schon das angestrebte Minimum erkennen lassen.
Die Minimumstruktur sieht für [Zn(sald)2] daher erwartungsgemäß nicht quadratisch-planar, sondern tetraedrisch aus:
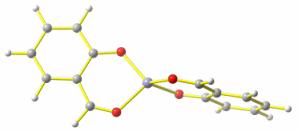
Abstände in Å von Zn zu: Ophen 1.93, Oald 2.01.
Neben der Struktur ein wichtiger Unschied zwischen den beiden Formen: die Gesamtenergie. Wird die Energie des stabilen Konformers auf 0 festgesetzt, errechnet sich der quadratisch-planare Übergangszustand auf B3LYP/tzvp-Niveau zu +40 kJ mol−1.
In auffallend vielen Kupfer-Enzymen gibt es ein T-förmiges CuN3-Chromophor. Beispiele aus der Vorlesung Bioanorganische Chemie sind Hämocyanin, CuZn-Superoxiddismutase und Cytochrom-c-Oxidase. Das N-Atom wird in diesen Enzymen von Histidin-Seitenketten zur Verfügung gestellt, die sich hinsichtlich ihrer Ligandeigenschaften nicht allzu sehr von Ammoniak unterscheiden. Wir überzeugen uns daher in einer DFT-Rechnung, dass das [Cu(NH3)3]2+-Ion wirklich T-förmig ist und fragen nach dem Grund.
Bei diesem Beispiel wird zur Berechnung Orca verwendet. In der Eingabedatei (cu3am.inp) wird das in Orca 4 implementierte CPCM-Modell (mit unendlicher Dielektrizitätskonstante) zur Modellierung einer Umgebung mit Standardparametern genutzt, des Weiteren werden van-der-Waals-Wechselwirkungen durch Grimmes Verfahren berücksichtigt. Wegen des Paramagnetismus wird „unrestricted“ gerechnet (α- und β-Spins mit unterschiedlicher Energie). Es bedeuten: uks [unrestricted Kohn-Sham], bp [BP86-Methode], ri [technisches Detail], d3 [Grimmes van-der-Waals-Korrektur], def2-tzvp [Basissatz], def2/j [Hilfsbasissatz für ri], opt [Strukturoptimierung, Computerchemiker sagen dazu „Geometrieoptimierung“], cpcm [Aufbau einer wasserartigen Umgebung]. Die nächsten vier Zeilen sorgen für die Übernahme aller nötigen Information in die Ausgabedatei, um Orbitale ansehen zu können. Mit „* xyz 2 2“ beginnt die Eingabe des Moleküls: xyz sagt kartesische Koordinaten an, die erste 2 ist die Ladung, die zweite 2 die Multiplizität).
Beständigkeitskonstanten von Komplexen können durch alle Methoden bestimmt werden, die eine Aussage zur Konzentration einer Spezies zulassen. Ein Standardverfahren für den häufigen Fall eines protonierbaren Liganden ist die Messung der H3O+-Konzentration, um die Konkurrenz eines Metallions und des Protons um den Liganden auszunutzen. Die Beständigkeitskonstanten werden dann durch Anpassen von Titrationskurven gewonnen. Mit bekannten Beständigkeitskonstanten können anschließend Speziesverteilungskurven errechnet werden.
Die wesentlichen Definitionen sind im zweiten Kapitel der Vorlesung Koordinationschemie zusammengesellt. Wie man nun in der Praxis vorgeht, schauen wir in einer Übung an, in der es wieder um Kupfer(II)-Komplexe geht. Der Ligand ist jetzt die proteinogene Aminosäure Serin. In der Übung werden die einzelnen Schritte gezeigt, wie das in den folgenden beiden Graphiken zusammengefasste Ergebnis erhalten wird. Als Hilfsmittel wird das Programm Hyperquad2008 verwendet. Auf eine Schwierigkeit mit der üblichen Art, Beständigkeitskonstanten protonendefizienter Spezies anzugeben, wird in einer pdf-Datei näher eingegangen.
Oben: Titration von 2 mmol Serin + 2 mmol H+ in 200 mL Lösung mit 0.5 m NaOH. Unten: Dieselbe Tritration nach Zusatz von 1 mmol Kupfer(II)-Salz.
[actae_retraction_2010]
IUCr: Retraction of articles.
Acta Crystallogr., Sect. Sect. E, 2010, 66, e21-e22.
doi:
10.1107/S1600536809054300.
Paramagnetische Metallzentren sind bevorzugte Motive, die in supramolekulare Strukturen einbaut werden. Dahinter steht die Hoffnung, magnetische Wechselwirkungen in ausgedehnten, aber wohldefinierten Strukturen zu erzeugen. In dieser Lehreinheit wird eine grundlegende Frage der Koordinationschemie beleuchtet: Führt ein räumlich enger Kontakt paramagnetischer Zentren zu einer magnetischen Wechselwirkung? – zu einer Bindung?
Um nebenbei koordinationschemische Grundregeln aufzugreifen, werden strukturell und chemisch nah verwandte Verbindungen betrachtet: Kupfer(II)- und Chrom(II)-acetat. Generell gilt, dass Kupfer(II)- und Chrom(II)-Verbindungen strukturell eng verwandt sind. Viele Salze sind isotyp. Ursache der Ähnlichkeit ist eine gemeinsame Besonderheit der d9- bzw. der high-spin-d4-Konfiguration. Beides sind bei oktaedrischer Koordination Jahn-Teller-Ionen, deren energetisch entartete Konfigurationen sich in der Besetzung des eg-Niveaus unterscheiden. Die Aufhebung der Degeneration bei diesen direkt auf die Liganden gerichteten Orbitale geht mit einer deutlichen Verzerrung des Koordinationsoktaeders einher, meist zu einer gestreckten quadratischen Bipyramide (Oh → D4h).
Ein Paar besonders interessanter Strukturen stellen die beiden Acetate von Kupfer(II) und Chrom(II) dar. Chrom(II)-acetat entsteht bei der Umsetzung von zum Beispiel Chrom(II)-sulfat, das bei der Umsetzung von hochreinem(?) Chrom mit hochreiner(?) Schwefelsäure entsteht, mit Natriumacetat. Aus dem blassblauen Hexaqua-chrom(II)-Ion entsteht rotes Chrom(II)-acetat-Monohydrat. Bei der Strukturanalyse überrascht der recht kurze Cr-Cr-Abstand von 2.36 Å.
Werden die Aqua-Liganden entfernt, sinkt der ohnehin schon kurze Abstand drastisch. Für die Gasphase ergibt die Elektronenbeugung an [Cr2(AcO)4] 1.96 Å. In kristallinem wasserfreien Chrom(II)-acetat beträgt der Cr-Cr-Abstand 2.29 Å (können Sie die merkliche Differenz zwischen Gasphase und Kristall erklären?).
Wird Acetat durch andere verbrückende Liganden ersetzt, so lässt sich der Metall-Metall-Abstand auf bis zu 1.828 Å verkürzen – vor der Entdeckung von Fünffachbindungen dem kürzesten bekannten Abstand zweier Metallatome überhaupt. Die Vorstellung einer kovalenten Bindung zwischen den Chrom-Atomen wird vor allem durch Verbindungen gestützt, bei denen eine Cr2-Einheit nicht durch Liganden überbrückt ist. So wird in einem ebenfalls roten und diamagnetischen Dichromat [Cr2R6]2− mit R = N,N-Dimethylaminomethyl ein Abstand von 1.84 Å zwischen den Chromatomen gefunden.
Wie sollte eine solche Bindung aussehen? Werden zwei isolierte, quadratisch-planare CrO4-Fragmente betrachtet, die in z-Richtung keine weitere Liganden tragen, so befinden sich die 4 Valenzelektronen in den d-Orbitalen xy, xz, yz und z2. Das bei quadratisch-planarer Koordination instabilste x2−y2-Orbital bleibt unbesetzt. Nähern sich die beiden Cr-Atome entlang z an, so kommt es zuerst zur Überlappung der z2-Orbitale, also zu einer σ-Bindung. Diese wird durch weitere Bindungen unterstützt, für deren Bildung symmetrie-geeignete Orbitale zur Verfügung stehen: zwei entartete π-Bindungen (xz ↔ xz und yz ↔ yz) sowie eine δ-Bindung aufgrund der Wechselwirkung der beiden xy-Orbitale. Die rote Farbe der Dichrom(II)-Verbindungen beruht auf einem δ→δ*-Übergang. Eine Bindungsordnung von 4 ist bei den Chrom-Verbindungen im großen und ganzen akzeptiert, auch wenn es Gegenargumente gibt. Man beachte, dass der gemessene Diamagnetismus auch erklärt werden kann, wenn zum Beispiel allein von einer σ-Bindung ausgegangen wird und die übrigen Spins durch Austausch-Kopplung zum S=0-Grundzustand führen.
Wie ist die Stärke der Chrom(II)-Chrom(II)-Vierfachbindung einzuschätzen? Hierzu gibt es den Bericht über den recht leichten Zerfall eines analogen Zweikernkomplexes beim einfachen Auflösen in kaum koordinierenden Lösungsmitteln. Trotz der Formulierung als Vierfachbindung ist die Wechselwirkung offensichtlich eher als schwach einzuschätzen.
Bei der ersten Metall-Metall-Vierfachbindung, die in der Literatur beschrieben ist, bestehen alle diese Zweifel nicht. Im Octachlorido-dirhenat(III), [Re2Cl8]2−, in dem die Rhenium-Atome trotz ihrer Stellung in der dritten Übergangsreihe nur 2.24 Å voneinander entfernt sind (vgl. 2.75 Å in Rhenium-Metall), liegen die Chlorido-Liganden in der sterisch ungünstigen ekliptischen Konformation vor, in der ihr Abstand kleiner als die Summe der van-der-Waals-Radien ist. Nur in dieser Anordnung ist eine δ-Bindung möglich. Wird in die langwellige Absorption, dem δ→δ*-Übergang, eingestrahlt, so kommt es im angeregten Zustand zur Rotation in die gestaffelte Konformation.
Gibt es eine Analogie zwischen Chrom(II)-acetat-Monohydrat und einem entsprechenden Kupfer(II)-acetat-Monohydrat? Auf den ersten Blick unbedingt. Die Strukturen weisen die gleiche Konnektivität und Symmetrie auf. Lediglich der Metall-Metall-Abstand ist bei der Kupferverbindung mit 2.612 Å weniger spektakulär (vgl. 2.56 Å im Metall) – was aber auch nicht zu erwarten ist, da bestenfalls eine Einfachbindung gebildet werden kann.
Eine Betrachtung des Kristallfeldschemas für ein quadratisch-planares CuO4-Fragment zeigt, dass das spintragende Orbital das x2−y2-Orbital ist. Die in Frage kommende Einfachbindung wäre also eine δ-Bindung. Die Art der Spinkopplung entspricht dagegen nicht ganz der Erwartung. Zwar ist im Grundzustand S = 0, allerdings lässt sich der Grundzustand nur bei tiefer Temperatur untersuchen; bei Raumtemperatur sind die beiden Spins merklich entkoppelt. Im Bereich teilweiser Spinkopplung zwischen ca. −200 und −100 °C beschreibt der Formalismus der antiferromagnetischen Kopplung korrekt den Verlauf der zunehmenden Entkopplung.
Die Struktur von Kupferacetat lässt die Interpretation durchaus zu, den S=0-Grundzustand als Folge antiferromagnetischer Kopplung zu verstehen. Die magnetischen x2−y2-Orbitale sind auf die O-Atome der verbrückenden Acetato-Liganden ausgerichtet und es ergibt sich ein antiferromagnetischer Austauschpfad im Sinne der Goodenough-Kanamori-Regeln, der im folgenden Bild für einen der vier Acetato-Liganden formuliert ist. Die übrigen drei Liganden lassen sich auf die gleiche Weise behandeln, so dass durch das Zusammenwirkung der vier Austauschpfade die hohe Kopplungskonstante von J = −294 cm−1 plausibel wird. (Die x-Richtung ist in der folgenden Abbildung senkrecht zur Zeichenebene gewählt, z verläuft entlang der Cu-Cu-Achse; man beachte, dass die px-Orbitale an den O-Atomen nichtbindende Wechselwirkungen mit den x2−y2-Orbitalen der Kupferatome aufweisen, dass also nicht die delokalisierte π-Bindung des Carboxylato-Liganden für die antiferromagnetische Kopplung verantwortlich ist; die üblicherweise formulierte sp2-Hybridisierung am Carboxylat-C-Atom wurde für das Kopplungsschema aufgehoben, ferner wurden die py- und pz-Orbitale der O-Atome in geeigneter Weise linearkombiniert; man beachter ferner eine alternative Darstellung magnetischer Kopplung am Beispiel des Fe2O-Kerns im Hämerythrin.)
Ist im Kupfer(II)-acetat nun eine δ-Bindung oder antiferromagnetische Spinkopplung für den S=0-Zustand verantwortlich? Das Schema suggeriert den derzeitigen Stand der Diskussion: Werden die Orbitale in der aus quantenchemischen Rechnungen erhaltenen Ausdehnung dargestellt, so ergibt sich bei dem schon recht großen Abstand der Kupferzentren keine nennenswerte direkte Überlappung der beiden magnetischen Orbitale, so dass die Übertragung der Spininformation auf dem abgebildeten Superaustauschpfad den bei weitem größeren Anteil an der beobachteten Spinkopplung haben dürfte. Wir betrachten hierzu die aktuelle Literatur.
pse11cu-cr-cu-oac_2020]
M. Malček, B. Vénosová, I. Puškárová, J. Kožíšek, M. Gall and L. Bučinský:
Coordination bonding in dicopper and dichromium tetrakis(μ-acetato)-diaqua complexes: Nature, strength, length, and topology.
J. Comput. Chem. 2020, 41, 698-714.
doi:
10.1002/jcc.26121
pse11cu-cr-cu-oac-xray_2018]
P. Herich, L. Bucinsky, M. Breza, M. Gall, M. Fronc, V. Petricek and J. Kozisek:
Electronic structure of two isostructural `paddle-wheel' complexes: a comparative study.
Acta Crystallographica Section B 2018, 74, 681-692.
doi:
10.1107/S2052520618013707
pse11-mm-bonding_2017]
P. Jerabek, B. von der Esch, H. Schmidbaur and P. Schwerdtfeger:
Influence of Relativistic Effects on Bonding Modes in M(II) Dinuclear Complexes (M = Au, Ag, and Cu).
Inorg. Chem. 2017, 56, 14624-14631.
doi:
10.1021/acs.inorgchem.7b02434
Das Fazit der Lehreinheit lautet, dass die d-Orbitale bei den Elementen der zweiten und dritten Übergangsreihe viel deutlicher den Charakter von Valenzorbitalen haben als bei den 3d-Elementen. Bei den Elementen der ersten Übergangsreihe sind die d-Orbitale näher am Atomrumpf lokalisiert und zeigen – umso mehr, wenn eine hohe Oxidationsstufe vorliegt – geringe Überlappung mit den Orbitalen der Bindungspartner. Paramagnetische, eventuell antiferromagnetisch gekoppelte, seltener ferromagnetisch gekoppelte Grundzustände sind daher bei vielen Komplexen mit 3d-Elementen die Regel, während 4d- und 5d-Metalle in homologen Verbindungen Metall-Metall-Bindungen aufbauen. Lanthanoide verhalten sich in dieser Hinsicht noch extremer als die Metalle der ersten Übergangsreihe. Hier stehen die teilweise besetzten f-Orbitale für eine Orbitalüberlappung nicht zur Verfügung, nicht einmal eine merkliche Kristallfeldaufspaltung trägt zur Chemie dieser Elemente bei.
Das Prinzip findet sich zum Beispiel bei Molybdän(V). In wässrig-saurer Lösung liegt eine kationische Spezies der Summenformel MoO2(H2O)3+ vor. In der Formulierung als Einkernkomplex läge ein d1-Zentrum vor – eine Situation, die bei den 3d-Elementen wohlbekannt ist, man denke an das Hexaaqua-titan(III)-Ion [Ti(H2O)6]3+ oder an das hydratisierte Pentaaqua-oxido-vanadium(IV)-Ion („Vanadyl“-Ion) [VO(H2O)5]2+. Mit dem 4d-Element Molybdän jedoch dimerisieren die hypothetischen d1-Radikale und es entsteht eine Mo-Mo-Einfachbindung:
Bei der Diskussion der Mo-Mo-Einfachbindung führt das Kristallfeldmodell zu einer plausiblen Deutung der Bindung als einer Wechselwirkung mit lokaler σ-Symmetrie. Sind die Liganden sehr verschieden oder ist die Struktur des Komplexes ungewöhnlich, fällt es schwerer, die metallständigen Orbitale hinsichtlich ihrer energetischen Abfolge zu ordnen. Ein Beispiel ist das [RuVINCl4]−-Ion, ein d2-Komplex, der aus RuO4, HCl und Azid zugänglich ist. Die Strukturanalyse zeigt quadratisch-pyramidalen Aufbau. Der Ru-N-Abstand ist mit 1.58 Å recht kurz. Die Bindungsverhältnisse lassen sich durch eine DFT-Rechnung (Orca 3) klären (Orca-Eingabe- und -Ausgabedatei ).
Auch hier wäre für eine Orca-4-Rechnung die erste Zeile zu ändern zu:
! rks bp ri def2-tzvp def2/j tightscf d3 cpcm(water)
Die Rechung auf bp/def2-tzvp-Niveau (van-der-Waals-Anziehung und wässrige Umgebung berücksichtigt) zeigt unter den fünf 4d-Orbitalen das z2-Orbital (64) als das unstabilste. Hier hätten wir es mit dem Kristallfeldmodell schwer gehabt zu entscheiden, ob der sehr nah an Ru gebundene Nitrido-Ligand die z-Richtung so sehr destabilisiert, dass auch die freie trans-Position dies nicht wieder ausgleicht. Hat man aber aus der Rechnung diesen Fixpunkt, ist die Orbitalreihenfolge klar: unter z2 finden wir x2−y2 (63), dann xz und yz (61 und 62), schließlich, als HOMO, xy (60). Ganz typisch für Komplexe der 4d- und 5d-Elemente: der Singulett-Zustand, hier ermöglicht durch die Ru-N-π-Wechselwirkungen. Im Bild ist deutlich der stark π-antibindende Charakter zu sehen, der die Orbitale 61 und 62 fast energiegleich mit dem x2−y2-Orbital (63) macht. Es resultiert ein so großer Energieunterschied zwischen den Orbitalen 60 und (61, 62), dass nur das stabilere unter Spinkopplung besetzt wird.
Das Fazit bis hierhin: dn-Zustände sind in der zweiten und dritten Übergangsreihe entweder Metall-Metall-bindend, oder sie führen zu low-spin-Konfigurationen.
Ein weiteres Beispiel für die d2-Konfiguration, nun aber Metall-Metall-Bindungen verursachend. Die Bindungsordnung zwischen den Molybdän(IV)-Atomen im dargestellten Tetrakation ist 1.
Die Tendenz zur Bildung von Metall-Metall-Bindungen wird bei den 4d- und 5d-Elementen herangezogen, um ungewöhnliche Eigenschaften zu deuten. Leitfähigkeitsmessungen zeigen zum Beispiel, dass in Kristallen von Nb3Cl8 1 bewegliches Elektron pro Formeleinheit vorliegt. In der Kristallstruktur liegen Nb3-Fragmente in Oktaederlücken einer dichtesten Chlorid-Packung vor. Die Ladung des Nb3-Fragments ist 8+, die formale Oxidationsstufe der Metallatome ist 8/3 entsprechend einer d-Elektronenzahl von 5 − 8/3 = 7/3. Werden nun jeweils 6/3 = 2 d-Elektronen für jeweils zwei Metall-Metall-Bindungen pro Niob-Atom verwendet, so bleibt 1/3 Elektron pro Niob-Atom, also 3 × 1/3 = 1 Elektron pro Formeleinheit übrig – passend zum Experiment:
Ein direkter Vergleich der d4-Zentren CrII und dem schweren Homologen MoII zeigt die Unterschiede zwischen der ersten und zweiten Übergangsreihe in besonders instruktiver Weise. Die Diskussion um Chrom(II)-acetat hat als Regel ergeben, dass Metall-Metall-Bindungen in den Strukturen sehr auffallend sind, aber hinsichtlich der Bindungsenergie nicht dominant sind. Ohne passgenau die Cr2-Einheit unterstützende Brückenliganden wird mit einer CrII-CrII-Bindung daher eher nicht zu rechnen sein.
An dieser Stelle gelingt der Bezug zur Festkörperchemie: Welcher Aufbau lässt sich aufgrund dieser Gesetzmäßigkeiten für Chrom(II)-chlorid ableiten? Welche Unterschiede sind zu erwarten, wenn anstelle von Chrom dessen schweres Homologes eingesetzt wird? Bei Molybdän(II)-chlorid treten nämlich die deutlich stärkeren MoII-MoII-Bindungen beim Aufbau des Festkörpers hervor.
Zurück zur Koordinationschemie: Welcher Aufbau darf für das Reaktionsprodukt von MoCl2 und 2 Cl− erwartet werden? Sind in ReCl3 = 1/3 Re3Cl9 Re-Re-Bindungen möglich?
Der Schwerpunkt des Kapitels lag auf Beispielen, bei welchen die Ausbildung von Metall-Metall-Bindungen als charakteristisches Verhalten der d-Elektronen von 4d- und 5d-Elementen auftrat. Generell ist diese Möglichkeit vor allem bei den frühen Übergangsmetallen zu finden. Verbindungen später, elektronenreicherer Metalle der zweiten und dritten Übergangsreihe sind durch low-spin-Zustände charakterisiert, die bei Bedarf von Metall-Metall-Bindungen begleitet werden. Das Prinzip wurde bereits bei [RuNCl4]− sichtbar. Als weiteres Beispiel werden Aufbau und Rh-Rh-Bindungsordnung in [Rh2(H2O)2(OAc)4] diskutiert.
Die in den beiden letzten Kapiteln diskutierten Fragen, ob eine Metall-Metall-Wechselwirkung in einem binuclearen Komplex durch eine ferro- oder antiferromagnetische Spinkopplung beschrieben werden sollte oder ob vielleicht von einer Bindung gesprochen werden sollte, ist immer dann nicht trivial, wenn die Metallatome recht nahe nebeneinander liegen – sie also nicht nur durch einen ausgedehnten Brückenliganden miteinander kommunizieren können. Die besprochenen Metall(II)-acetate sind solche Beispiele. Ein Brückenligand ist vorhanden und bietet Superaustauschpfade, der M–M-Abstand aber liegt im Bereich des Atomabstands im Metall selbst und könnte eine Bindung anzeigen.
Das übliche Routineverfahren, mit geringem Aufwand die Austauschwechselwirkung von Metallatomen zu berechnen, ist eine broken-symmetry-DFT-Rechnung (BS-DFT). Das Verfahren ist einfach und „billig“ im Sinne geringer Rechnerressourcen, hat aber für die Lehre den Nachteil, dass der dort verwendete broken-symmetry-Zustand wenig anschaulich ist. Zuerst aber der technische Teil. Wir verwenden Orca, um zuerst die jeweilige Molekülstruktur zu optimieren (lässt man in der Literatur oft auch weg und fixiert den M-M-Abstand auf den gefundenen Wert; hier wurden die drei Strukturen mit bp/tzvp + d3 + cosmo(water) verfeinert, also reines Dichtefunktional mit nicht zu teurem Basissatz, Grimmes van-der-Waals-Korrektur [d3] und Kontinuummodell mit der Dielektrizitätskonstante von Wasser); im Detail wird optimiert: Cu im BS-Zustand, Cr auch, Rh im spingepaarten Singulettzustand.
Anschließend werden mit dem tpssh-Hybridfunktional und def2-tzvp (außerdem wie zuvor d3 und cosmo) Eingabedateien geschrieben für Cu, Cr, Rh und dabei die Atomkoordinaten aus den Optimierungen verwendet.
Bei der Rechnung wird nun dem ferromagnetisch gekoppelten Zustand (in der Literatur leider „high-spin“ genannt) ein broken-symmetry-Zustand gegenübergestellt, indem die Spins an dem Zentrum mit der geringeren Zahl ungepaarter Elektronen herumgedreht werden; sind wie hier die beiden Zentren gleich, ist es egal welches. In der Orca-Eingabedatei geht das so: Die Multiplizität, die wie üblich der letzte Eintrag auf der xyz-Anweisung ist, gilt für den ferromagnetisch gekoppelten Zustand. Bei Cu steht daher eine „3“, da die beiden α-Spins dann ein Triplett bilden. Bei Chrom(II) sind die beiden Bausteine high-spin-d4 („high-spin“ jetzt wieder individuell), beide zusammen in ferromagnetischer Kopplung also S = 2 + 2 = 4, 2S + 1 = 9, und: *xyz 0 9. Für Rhodium(II) gehen wir von zwei Zentren aus, die jedes für sich low-spin-d7 sind, also 1 Spin pro Zentrum, die zusammen wie bei Kupfer(II) ein Triplett ergeben.
Anschließend wird der broken-symmetry-Zustand eingerichtet, und zwar zwischen „%scf“ und „end“: flipspin 1 heißt: drehe die Spins von Atom 1 um (das ist bei Orca, bei dem Aufzählungen immer mit 0 beginnen, das zweite Atom in der Liste). Dann: finalms 0, lies: final Ms = 0, womit die Spinorientierungsquantenzahl im antiferromagnetisch gekoppelten Zustand angegeben wird.
%scf
flipspin 1
finalms 0
end
* xyz 0 3
Cu ...
Cu ...
...
Das Programm geht jetzt hin und beginnt mit der ferromagnetisch gekoppelten Anordnung. Anschließend werden die Spins umgedreht und es wird versucht, in einer unrestricted-Rechnung („uks“ = unrestricted Kohn Sham) von diesem antiferromagnetisch gekoppelten Zustand zu retten, was in einer DFT-Rechnung zu retten ist. Im Falle magnetischer Kopplung kommt dann ein broken-symmetry-Zustand heraus, der stark vom Erwartungswert für S(S+1)=0 abweicht (Tabelleneintrag <S2>BS). Man sagt, dass er „spinkontaminiert“ sei. Energetisch liegt er zwischen dem wahren antiferromagnetisch gekoppelten und dem ferromagnetisch gekoppelten Zustand (der Hintergrund der Geschichte ist, dass der antiferromagnetisch gekoppelte Zustand im Gegensatz zum ferromagnetisch gekoppelten Zustand ein Multikonfigurationszustand ist, der sich durch DFT-Methoden nicht darstellen lässt). Erstaunlicherweise ergibt sich die Kopplungskonstante J aus einer solchen Rechnung oft ganz gut; schauen Sie sich ziemlich am Ende der Ausgabedateien den Wert für J(3) an, der als Energiedifferenz zwischen ferromagnetisch gekoppeltem und broken-symmetry-Zustand dividiert durch die Differenz der <S2>-Werte für die beiden Zustände berechnet wird (der experimentelle Wert bei der Kupferverbindung wird zwischen −290 und −300 cm−1 angegeben).
Sie finden alles in den out-Dateien für Cu, Cr, Rh (die out-Dateien sind sehr lang, da sie die gesamte Orbitalinfomation enthalten, falls Sie sich zum Beispiel in Gabedit Orbitalwechselwirkungen anschauen wollen).
Nach diesen wenig befriedigenden rechentechnischen Details können wir aber jetzt auf den Punkt kommen – und dabei viele Aussagen wiederentdecken, die wir zuvor qualitativ gemacht haben. Wir schauen dazu die folgende Tabelle an, in der J das J(3) der Rechnung ist. Sehr nützlich ist der Eintrag Sαβ, der ein Überlappungsintegral darstellt, das in Orca in einer Auflistung von „Corresponding Orbitals“ zu finden ist (cave: auch Orbitale zählen in Orca ab 0, beim Anschauen in Gabedit ab 1 (Sαβ wird in der Literatur meist ohne „αβ“ hingeschrieben). Sαβ = 0 sagt uns: keine Überlappung, Sαβ = 1 heißt: ein ganz normales spingekoppeltes Elektronenpaar (das sind mit Abstand die meisten in der Liste), 0 < Sαβ < 1: zeigt ein mehr (ca. 0) oder weniger (ca. 1) spinpolarisiertes Elektronenpaar an. Der Zahlenwert bei Cu von 0.17 ist dabei keine Überlappung von zwei allein auf Kupfer liegenden Atomorbitalen, sondern es ist die Überlappung zwischen einem α-MO und einem β-MO, die sich auch über die Brückenliganden hinweg erstrecken. Zusammen mit dem negativen Vorzeichen von J sieht so eine durch Superaustausch vermittelte antiferromagnetische Spinkopplung aus.
Das Gegenstück ist der Rhodiumkomplex. Hier war Ihnen erzählt worden, dass es sich um eine normale Rh-Rh-Bindung handelt, man würde sich also eine broken-symmetry-Rechung ersparen und das ganze (restricted) als normales Singulett behandeln (so wurde die Struktur optimiert). Macht man aber überflüssigerweise eine broken-symmetry-Rechnung, kommt ein klares Ergebnis heraus: der BS-Zustand ist nicht spinkontaminiert (<S2>BS = 0), der ferromagnetisch gekoppelte diradikalische Zustand ist extrem unstabil (siehe J in kJ mol−1), und das Überlappungsintegral ist 1. (Wir nutzen die Rechnung, um als Einschub einen näheren Blick auf die low-spin-d7-Situation zu werfen und sie mit dem Hauptgruppen-7-Valenzelektronen-Fall des Chlors zu vergleichen.)
Und der Chromkomplex, dem die Literatur die hohe Bindungsordnung 4 zuweist, die Bindung dann aber gleich wieder als sehr schwach einstuft? Schauen Sie hier vor allem auf die vier Überlappungsintegrale im Grenzorbitalbereich, die in der Tabelle in σ, π (in der Orca-Ausgabe die beiden vorletzten Einträge) und δ unterschieden sind. Man kommt zu dem Schluss, dass nur die σ-Bindung nennenswert ist, aber wie bei Kupfer ist auch hier J eher bescheiden, wenn wir uns das Ergebnis auf einer Kilojoule-pro-Mol-Skala klar machen. Ganz interessant: die δ-Wechselwirkung stellt sich beim Kupfer- und beim Chromkomplex sehr ähnlich dar.
| CuII (d9) | CrII (d4) | RhII (d7) | |
|---|---|---|---|
| M-M/Å (Xray) | 2.612 | 2.362 | 2.386 |
| M-M/Å (DFT) | 2.529 | 2.290 | 2.430 |
| J/cm−1 | −309 | −809 | −6380 |
| J/kJ mol−1 | −3.7 | −9.7 | −76.3 |
| <S2>BS | 0.97 | 3.27 | 0.00 |
| Sαβ (σ) | – | 0.73 | 1.00 |
| Sαβ (π) | – | 0.29 | – |
| Sαβ (δ) | 0.17 | 0.19 | – |
Zum Schluss noch einmal der Hinweis: der Rhodiumkomplex würde in einer Publikation sicher nicht eine broken-symmetry-Behandlung erfahren.
con-bs-spin-coupling_2018]
G. David, F. Wennmohs, F. Neese and N. Ferré:
Chemical Tuning of Magnetic Exchange Couplings Using Broken-Symmetry Density Functional Theory.
Inorg. Chem. 2018, 57, 12769-12776.
doi:
10.1021/acs.inorgchem.8b01970
High-spin-Cobalt(II) illustriert besonders anschaulich das Prinzip, dass die d-Elektronen der 3d-Elemente nur begrenzt die Chemie dieser Zentralmetalle mitbestimmen, sich also wie Valenzelektronen verhalten. Metall-Metall-Bindungen werden nicht beobachtet, darüber hinaus bedingt die ungefähr gleiche Ligandfeldstabilisierungsenergie bei verschiedenen Koordinationsfiguren, dass Kristallfeldeffekte kaum wahrnehmbar sind.
Dies alles gilt jedoch nur im high-spin-Fall. Starkfeldliganden, die eine d7-low-spin-Anordnung verursachen können, verändern dieses Bild völlig. [Co(CN)4]2− ist quadratisch planar, [Co(CN)5]3− neigt zur Dimerisierung zu [Co2(CN)10]6− unter Aufbau einer Co-Co-Bindung, ein dem [Fe(CN)6]4− entsprechendes [Co(CN)6]4− ist nicht bekannt. Vor allem die Bildung einer Metall-Metall-σ-Bindung bei der Dimerisierung rückt das low-spin-Cobalt(II) in die Nähe seiner schweren Homologen. Völlig analog bildet Rhodium(II) eine Rh-Rh-σ-Bindung im oben erwähnten [Rh2(H2O)2(OAc)4].
Der Unterschied zwischen Cyanido- und Halogenido-Liganden wird im Orbitalschema deutlich. Halogenido-Liganden sind σ- und π-Donoren. Cyanido-Liganden sind bessere σ-Donoren, deren HOMO, das 3σ-Orbital, wirksam auf das Zentralmetall zuweist. Das HOMO−1, das 1π-Orbital, ist dagegen auf das elektronegativere N-Atom ausgerichtet, so dass dessen Überlappung mit dem Zentralmetall schwach ist (vgl. die analoge Situation bei den Grenzorbitalen des Carbonyl-Liganden). Cyanid ist also aufgrund seines Aufbaus aus einem elektronegativen N- und einem weniger elektronegativen C-Atom ein Ligand, dessen σ-Donoreigenschaft verstärkt und dessen π-Donoreigenschaft geschwächt ist.
Beides trägt zur Stellung des Cyanido-Liganden in der spektrochemischen Reihe bei. Liegt ein Zentralmetall in niedriger Oxidationsstufe vor, kommt ein weiterer Aspekt hinzu, der in der Literatur jedoch kontrovers behandelt wird. Das LUMO, das 2π-Orbital, ist ebenfalls deutlich auf das Zentralmetall ausgerichtet. Dessen Symmetrie erlaubt eine Überlappung mit lokaler π-Symmetrie mit geeigneten d-Orbitalen des Zentralmetalls, bei einem oktaedrischen Komplex mit den t2g-Orbitalen. Sind diese besetzt, wird eine Rückbindung erhalten. Das Metall wirkt hierbei als Lewis-Base, der Ligand als Säure. In der Summe zeigt sich Cyanid als starke σ-Base, als schwache π-Base und eventuell als π-Säure, wenn geeignete besetzte Orbitale am Zentralmetall zur Verfügung stehen. Unter welchen Umständen eine π-Rückbindung einen merklichen Beitrag hat, ist Gegenstand der Diskussion. Aus Röntgenspektren wurde abgeleitet, dass selbst low-spin-Eisen(II) im Hexacyanidoferrat(II) trotz seiner recht hohen Oxidationsstufe und seiner folglich eher stärker kontrahierten 3d-Orbitale eine „nennenswerte“ Rückbindung aufbauen [cyano_2001].
Die bei den Cyanidocobaltaten(II) gefundenen Verhältnisse zumindest lassen sich zwanglos mit der starken σ-Basizität der Cyanido-Liganden allein erklären. In einem oktaedrischen [Co(CN)6]4− wäre die Aufspaltung zwischen eg und eg* groß, eg* wäre stark antibindend. In dieses Schema sind 7 + 6 × 2 = 19 Elektronen einzufüllen, 1 Elektron würde sich also – anders als im [Fe(CN)6]4−-Ion – im stark antibindenden Zustand wiederfinden. Komplexe mit stark σ-basischen Liganden, zu denen zum Beispiel auch Hydrido- und Alkyl-Liganden zählen, beachten daher eine Obergrenze von 18 Elektronen. Im Fall des [Co(CN)4]2−-Ions führt die gleiche Betrachtung zur quadratisch-planaren Ligandanordnung anstelle der tetraedrischen. Auch ist es günstig, bei starkem Feld das stark antibindende x2−y2-Orbital nicht zu besetzen. Bei tetraedrischer Anordnung gibt es dagegen kein einzelnes unstabiles Orbital.
Die qualitativen Aussagen, vor allem die sich häufiger ändernde Einschätzung, ob eine Rückbindung in Cyanidokomplexen von Metallen in positiver Oxidationsstufe nennenswert ist oder nicht, sollen anhand dreier Komplex-Ionen näher betrachtet werden. Nebenbei wenden wir eine weiter oben schon vorgestellte Publikation an, mit deren Hilfe die möglichen Spinzustände eines Formeltyps eingegrenzt werden [orbital_deformation_2006] und gehen der Frage nach, ob das Erstaunen der Autoren von [cyano_2005] gerechtfertigt ist, das erste high-spin-Cyanidochromat hergestellt zu haben. Die Formel des high-spin-Chromats ist [Cr(CN)5]3−; im Kristall liegen quadratisch-planare Konformere neben verzerrt trigonal-bipyramidalen vor. Die fünf α-Spin-d-Orbitale spalten in der folgenden Weise auf:
Die Aufspaltung der d-Orbitale im high-spin-Cyanido-Komplex [CrII(CN)5]3− für die beiden Konformere (bp/tzvp). Die vier stabilen Orbitale enthalten ein Elektron.
Wir diskutieren als Erstes, warum bei der d4-Konformation die Spinzustände S = 0 und 1 nicht vorkommen sollen, sondern nur S = 2. Anschließend gehen wir auf einen weiteren Punkt der Publikation ein, und zwar auf die Bedeutung von s- und p-Orbital-Zumischungen zu d-Orbitalen. Hierzu betrachten wir das quadratisch-pyramidale Konformer (SPY-5):
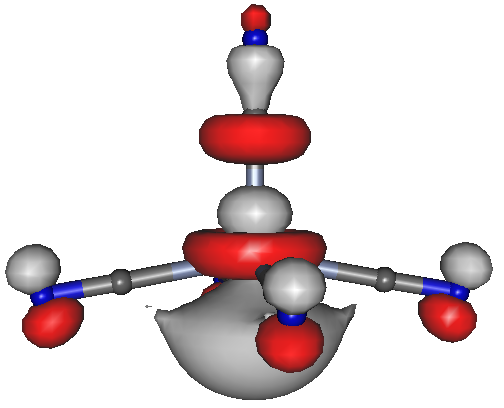
Der high-spin-Cyanido-Komplex [CrII(CN)5]3−, HOMO (Orbital 48a) des C4v-Konformers (auf bp/tzvp-Niveau 3.2 kJ mol−1 unstabiler als das D3h-Konformer); isovalue = 0.04.
Nun zur Frage der Rückbindung. Das α-MO 45 sollte eine solche Bindung zeigen, sie scheint aber keine besondere Bedeutung zu haben:
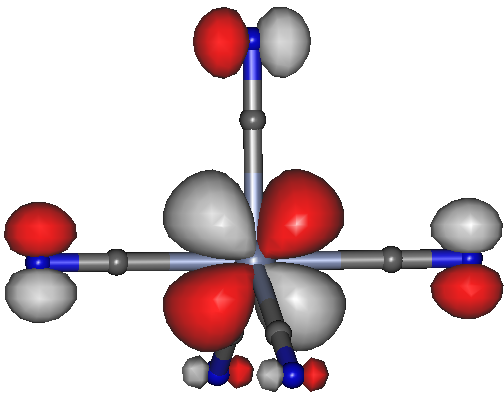
[CrII(CN)5]3−, Orbital 45a des D3h-Konformers; isovalue = 0.04.
Man könnte einwenden, dass zu einer richtigen Rückbindung Elektronenpaare gehören, die der high-spin-d4-Komplex nicht zu bieten hat. Wir vergleichen daher das analog aufgebaute low-spin-d8-Ion [NiII(CN)5]3−:
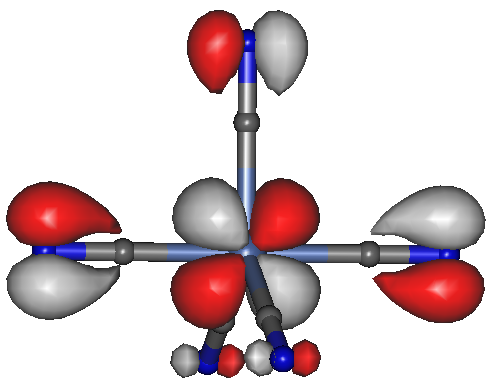
Das D3h-Konformer des [NiII(CN)5]3−-Ions, Orbital 45a (das C4v-Konformer ist auf bp/tzvp-Niveau 0.6 kJ mol−1 unstabiler; isovalue = 0.04.
Auch hier zeigt sich keine nennenswerte Rückbindung. Zum Vergleich schauen wir auf das [Cr(CO)5]2−-Ion, das alle Voraussetzungen für eine Rückbindung mit sich bringt: die Oxidationsstufe des Metalls ist sehr niedrig, der Ligand ist CO.
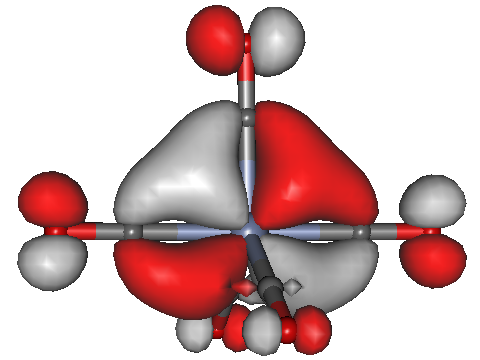
[Cr(CO)5]2−, Orbital 45a; isovalue = 0.04.
Tatsächlich ist es nun überhaupt kein Problem, die Delokalisation des Metall-Orbitals auf die C-Atome der Carbonylliganden zu erkennen.
Das Fazit: bei positiver Oxidationsstufe des Metalls und Cyanid als Ligand ergibt sich die große Kristallfeldaufspaltung aus der Kovalenz der M-C-Bindung, nicht aus einer Rückbindung. Die hohe σ-Basizität unterscheidet den Cyanido-Liganden von isosteren Teilchen wie CO und NO+. Man vergleiche hierzu die Stabilitäten von HCN und HCO+. Trotz der formalen Gemeinsamkeiten unterscheidet sich die Carbonyl-Komplexchemie erheblich von der Cyanid-Metall-Chemie. Stabile Cyanido-Komplexe von Metallen mit positiver Oxidationsstufe gibt es in großer Zahl, nicht jedoch die analogen Carbonylkomplexe. Man vergleiche [Cu(CN)4]3− und einen der unbeständigen Carbonyl-kupfer(I)-Komplexe wie [Cu(NH3)3(CO)]+ oder Cu(CO)Cl.
Besonders illustrativ ist der Vergleich zwischen [Fe(CN)6]4− und [Fe(CO)6]2+. Das Anion des gelben Blutlaugensalzes ist seit fast 200 Jahren bekannt; es ist so stabil, dass es ungiftig ist. Das Hexa(carbonyl)eisen(II)-Ion wurde dagegen erst kürzlich von Willner und Aubke in supersauren Medien hergestellt, also in Abwesenheit aller konkurrierender Liganden. Stabile Carbonylmetall-Komplexe sind dagegen unter Bedingungen bekannt, die die höhere π-Acidität des Kohlenmonoxids ausnutzen, also mit Metallen in niedriger Oxidationsstufe, die eine hinreichend große Metallbasizität aufbringen, um die M-CO-Rückbindung zu stärken. Komplexe mit dem NO+-Ligand setzen diesen Trend fort. Beständige Nitrosyl-Komplexe vom NO+-Typ sind daher nur von elektronenreichen Metallen bekannt.
pse2-m8co_2018]
X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking:
Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr, or Ba) that mimic transition metals.
Science 2018, 361, 912-916.
doi:
10.1126/science.aau0839
pse2-m8co-report_2018]
P. B. Armentrout:
18 electrons and counting.
Science 2018, 361, 849.
doi:
10.1126/science.aau6622
pse2-m8co-comment_2019]
C. R. Landis, R. P. Hughes and F. Weinhold:
Comment on Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr, or Ba) that mimic transition metals.
Science 2019, 365, eaay2355.
doi:
10.1126/science.aay2355
pse2-m8co-reply_2019]
L. Zhao, S. Pan, M. Zhou and G. Frenking:
Response to Comment on Observation of alkaline earth complexes M(CO)8 (M = Ca, Sr, or Ba) that mimic transition metals}.
Science 2019, 365, eaay5021.
doi:
10.1126/science.aay5021
pse2-octacarbonyl-qtaim-elf_2020]
J. F. Van der Maelen:
Topological Analysis of the Electron Density in the Carbonyl Complexes M(CO)8 (M = Ca, Sr, Ba).
Organometallics 2020, 39, 132-141.
doi:
10.1021/acs.organomet.9b00699
pse2-octacarbonyl-qtaim-elf-comment_2020]
N. Holzmann, I. Fernández and G. Frenking:
Comment on Topological Analysis of the Electron Density in the Carbonyl Complexes M(CO)8 (M = Ca, Sr, Ba).
Organometallics 2020, 39, 2956-2958.
doi:
10.1021/acs.organomet.0c00419
pse2-octacarbonyl-qtaim-elf-reply_2020]
J. F. Van der Maelen:
Response to Comment on Topological Analysis of the Electron Density in the Carbonyl Complexes M(CO)8 (M = Ca, Sr, Ba).
Organometallics 2020, 39, 3458-3460.
doi:
10.1021/acs.organomet.0c00523
pse2-ca8co_2019]
D. Koch, Y. Chen, P. Golub and S. Manzhos:
Revisiting π backbonding: the influence of d orbitals on metal--CO bonds and ligand red shifts.
PCCP 2019, 21, 20814-20821.
doi:
10.1039/C9CP04624K
pse2-ca8co-comment_2020]
S. Pan and G. Frenking:
Comment on Revisiting π backbonding: the influence of d orbitals on metal--CO bonds and ligand red shifts by D. Koch, Y. Chen, P. Golub and S. Manzhos, \textit{Phys. Chem. Chem. Phys.}, 2019, 21, 20814.
PCCP 2020, 22, 5377-5379.
doi:
10.1039/C9CP05951B
pse2-ca8co-reply_2020]
D. Koch, Y. Chen, P. Golub and S. Manzhos:
Reply to the Comment on Revisiting π backbonding: the influence of d orbitals on metal--CO bonds and ligand red shifts by G. Frenking and S. Pan, \textit{Phys. Chem. Chem. Phys.}, 2019, 22, DOI: 10.1039/C9CP05951B.
PCCP 2020, 22, 5380-5382.
doi:
10.1039/C9CP06927E
pse2-m8n2_2019]
Q. Wang, S. Pan, S. Lei, J. Jin, G. Deng, G. Wang, L. Zhao, M. Zhou and G. Frenking:
Octa-coordinated alkaline earth metal–dinitrogen complexes M(N2)8 (M = Ca, Sr, Ba).
Nature Communications 2019, 10, 3375.
doi:
10.1038/s41467-019-11323-5
pse2-m8co-m8n2_2020]
T. Bettens, S. Pan, F. De Proft, G. Frenking and P. Geerlings:
Alkaline Earth Metals Activate N2 and CO in Cubic Complexes Just Like Transition Metals: A Conceptual Density Functional Theory and Energy Decomposition Analysis Study.
Chem. Eur. J. 2020, 26, 12785-12793.
doi:
10.1002/chem.202001585
con-os-eos-loba_2020]
M. Gimferrer, J. Van der Mynsbrugge, A. T. Bell, P. Salvador and M. Head-Gordon:
Facing the Challenges of Borderline Oxidation State Assignments Using State-of-the-Art Computational Methods.
Inorg. Chem. 2020, 59, 15410-15420.
doi:
10.1021/acs.inorgchem.0c02405
[con_oxidationstate_2018]
V. Postils, C. Delgado-Alonso, J. M. Luis and P. Salvador:
An Objective Alternative to IUPAC's Approach To Assign Oxidation States.
Angew. Chem. Int. Ed. 2018, 57, 10525–10529.
doi:
10.1002/anie.201802745
iupac_oxidation_state_2016]
P. Karen, P. McArdle and J. Takats:
Comprehensive definition of oxidation state (IUPAC Recommendations 2016).
Pure & Applied Chemistry 2016, 88, 831–839.
doi:
10.1515/pac-2015-1204
[fe3co1no_2014]
J. E. M. N. Klein, B. Miehlich, M. S. Holzwarth, M. Bauer, M. Milek, M. M. Khusniyarov, G. Knizia, H.-J. Werner and B. Plietker:
Der elektronische Grundzustand von [Fe(CO)3(NO)]−: eine spektroskopische und theoretische Studie.
Angew. Chem. 2014, 126, 1820–1824.
doi:
10.1002/ange.201309767
[orbital_deformation_2006]
S. Alvarez, J. Cirera:
How High the Spin? Allowed and Forbidden Spin States in Transition-Metal Chemistry.
Angew. Chem. Int. Ed. 2006, 45, 3012–3020.
doi:
10.1002/anie.200503492
[cyano_2005]
K. J. Nelson, I. D. Giles, W. W. Shum, A. M. Arif, J. S. Miller:
The Myth of Cyanide Always Being a Strong-Field Ligand: Synthesis and Structural Characterization of Homoleptic S = 2 Pentacyanidochromate(II), [CrII(CN)5]3−, and Nonacyanidodichromate(II), [CrII2(CN)9]5−.
Angew. Chem. 2005, 117, 3189–3192.
doi:
10.1002/ange.200462763
So etabliert und nützlich die 18-Elektronen-Regel als Richtschnur in der Koordinationschemie und der metallorganischen Chemie auch ist, so unsicher sind manche konkreten Aussagen zur Bindungssituation eines Komplexes. Einer der kritischsten Punkte betrifft die Natur der postulierten Bindungen zwischen 3d-Metallen. In den DFT-Rechnungen, die weiter oben zur Analyse der CO-Valenzschwingungen von Fe2(CO)9 vorgenommen wurden, findet man eine Fe-Fe-Bindung nicht ohne Weiteres. Da wir bisher Ausagen zur Elektronenstruktur immer nur aus der MO-Behandlung eines oktadrischen Komplexes abgeleitet hatten, soll in diesem Abschnitt der 18-Elektronenfall bei einem tetraedrischen Carbonylkomplex analysiert werden, und zwar bei Tetracarbonylnickel(0). Anschließend sollen die dort gewonnenen Verallgemeinerungen genutzt werden, um in einer DFT-Rechnung nach der Eisen-Eisen-Bindung zu suchen, die durch die Abzählregeln für Fe2(CO)9 gefordert wird.
Nickel trägt 28 Elektronen zu Tetracarbonylnickel bei, die vier Carbonylliganden insgesamt 56 Elektronen. Eine All-Elektronen-Rechnung am diamagnetischen Carbonylkomplex ergibt also 42 doppelt besetzte Orbitale. Davon sind 17 Elektronenpaare stabile Rumpfelektronenpaare (Ni: 1s, 2s, 3 × 2p, 3s, 3 × 3p; außerdem 8 × 1s der Leichtatome), des Weiteren darf man die aus der bindenden und antibindenden Wechselwirkung der 2s-Orbitale von C und O resultierenden Orbitale 1σ und 2σ des freien CO als so stabil ansehen, dass diese 8 MOs im Schema wohl folgen werden. Wir betrachten daher die Orbitale 26–42. Um sie zuzuordnen, sollte man die Gestalt der CO-Grenzorbitale vor Augen haben, dem aus C(2pz) und O(2pz) entstandenen 3σ sowie den beiden bindenden π-Orbitalen 1π und 2π.
Die Zuordnung der 17 Orbitale (wir verwenden GaussView und die formatierte Checkpointdatei einer b3lyp/tzvp-Rechnung, die Sie mit dieser Eingabedatei selbst nachvollziehen können oder deren Protokolldatei Sie ansehen können) ist übersichtlich, auch wegen der hohen Symmetrie (Td). In der folgenden Tabelle markiert n den Beitrag zur 18-Elektronenbilanz:
| MO | Sym. | Zuordnung | n |
|---|---|---|---|
| 40, 41, 42 | t2 | Ni(xy,xz,yz) (π-Rückbindungen) | 6 |
| 38, 39 | e | Ni(z2, x2−y2) π-Rückbindungen | 4 |
| 35, 36, 37 | t2 | CO(3σ) + Ni(3d,4p) | 6 |
| 32, 33, 34 | t1 | CO(π) | 0 |
| 29, 30, 31 | t2 | CO(π) | 0 |
| 27, 28 | e | CO(π) | 0 |
| 26 | a1 | CO(3σ) + Ni(4s) | 2 |
Es lassen sich einige Regeln erkennen: Bei der Anwendung der 18-Elektronenregel werden mögliche π-Donor-Bindungen nicht mitgezählt. Die entsprechenden Orbitale 27–34 (e + t2 + t1) haben auch nahezu reinen Ligandcharakter. Die übrigen Orbitale schließen die Nickel-Valenzorbitale (3d, 4s, 4p) ein: entsprechend den vier Donor-Elektronenpaaren der vier CO-Liganden treten die vier MOs 26 und 35–37 auf (a1 und t2). Daneben gibt es die 3d-Elektronenpaare an Nickel (e, t2), die als einsame Elektronenpaare gesehen werden können, die ihre Elektronendichte im Sinne von Rückbindungen aber auch in CO(π*)-Orbitale delokalisieren können.
In einer VB-Betrachtung würde man ein Nickelatom mit 5 freien Elektronenpaaren zeichnen, sowie 4 koordinative Bindungen, die von den CO-Liganden ausgehen und 4 sp3-Hybridorbitale am Zentralatom füllen. Hinzu kämen nun etliche mesomere Grenzstrukturen, um die Rückbindungen zu berücksichtigen.
Eine alternative Methode zur Interpretation der Wellenfunktion eines Moleküls ist die Analyse der Elektronendichte, wobei diese experimentell oder computerchemisch ermittelt worden sein kann. Die wohl am weitesten verbreitete Methode ist die Quantum Theory of Atoms in Molecules, kurz QTAIM. Wir diskutieren das Prinzip und das Ergebnis für Decacarbonyldimangan am Beispiel einer aktuellen Publikation [qtaim_2016].
Nun zum heikleren Fall Nonacarbonyldieisen(0). Die 18-Elektronenformulierung führt hier zu einer Fe-Fe-Einfachbindung (2 × 8 e− + 8 × 2 e− = 34 e− entsprechend 17 e− pro Eisenatom; wie bei einem 7-e−-Chloratom wird also Dimerisierung unter Ausbildung einer Einfachbindung erwartet). Eine DFT-Rechnung auf demselben Niveau wie zuvor (Eingabedatei, Protokolldatei) führt zu 89 doppelt besetzten Orbitalen. Werden die 36 Rumpfelektronenpaare abgezogen, verbleiben 53 Valenzelektronenpaare. Da das Tetracarbonylnickel-Beispiel gezeigt hatte, dass alle CO-Orbitale unterhalb des Grenzorbitalbereichs lagen, subtrahieren wir noch einmal 5 × 9 = 45 Orbitale. Es verbleiben jetzt 8 Grenzorbitale. Bevor diese analysiert werden, hier noch die Gegenprobe:
Die 18-Elektronenregel betrachtet die 2 × 9 = 18 Valenzorbitale (2 × 4s, 6 × 4p, 10 × 3d) der beiden Eisenatome. Da 2 × 17 e− zur Verfügung stehen, sind im Singulett-Molekül Fe2(CO)9 17 besetzte Valenzorbitale zu berücksichtigen. Zu diesen zählen auch die 9 Orbitale mit Metall-s- und -p-Charakter, die durch die 9 Donorbindungen der 9 CO-Liganden gefüllt werden. Im Grenzorbitalbereich bleiben 17 − 9 = 8 Orbitale – die wir nun endlich anschauen wollen.
Wir laden die formatierte Checkpointdatei einer b3lyp/tzvp-Rechnung in der Punktgruppe D3h wieder mit GaussView:
| MO | Sym. | Zuordnung |
|---|---|---|
| 88, 89 | e′′ | Fe(x2−y2, z2), Fe-μ-CO(π*)-Rückbindungen |
| 87 | a2′′ | Antibindung zu 84! |
| 85, 86 | e′′ | Antibindung zu 82, 83! |
| 84 | a1′ | Fe(xy,xz,yz), die Fe-Fe-Bindung |
| 82, 83 | e′ | Fe(xy,xz,yz), Fe-Fe-bindend |
Es zeigt sich, dass es zu jeder Fe-Fe-bindenden Wechselwirkung eine antibindende Wechselwirkung gibt. In der Literatur wird dementsprechend seit Jahrzehnten um die Fe-Fe-Bindung gestritten. In der neuesten verfügbaren Arbeit [fe2co9_bonding_2007] wird eine schwache Bindung gefunden und zwar so: man betrachte vor allem Bindung (MO 84) und Antibindung (MO 87) genauer. Die Antibindung weist an den Brückencarbonyl-Liganden höhere Koeffizienten auf, sie ist in eine Wechselwirkung zu CO(π*)-Orbitalen delokalisiert. Durch die Beteiligung an der Rückbindung schwächt sie die Fe-Fe-Bindung weniger.
Im VB-Formalismus entspricht ein doppelt besetztes Molekülorbitalpaar jeweils einem freien Elektronenpaar an jedem Atom. Man würde also die MOs 84 und 87 an das Fe-Atompaar lokalisieren, indem man jedem Fe-Atom ein freies Elektronenpaar zuweist. Hinzu kommen nun mesomere Grenzformen, in denen eine Fe-Fe-Bindung formuliert wird und das zweite Elektronenpaar für eine Rückbindung zu einem Brücken-CO-Liganden verwendet wird. Die 18-Elektronenregel gilt dabei nur für die Fe-Fe-gebundenen Formen (siehe auch Fig.41ff in 3z2e_bonds_2012]).
Das hier geschilderte Problem zeigt die Grenzen einer strikten Isolobalbehandlung. Es tritt gehäuft auf, wenn in Mehrkernkomplexen von 3d-Zentralmetallen Donor/Akzeptor-Brückenliganden vorkommen.
Es ist schon verrückt: N2 ist viel schwerer zu reduzieren als das isostere CO, trotzdem befasst sich die Koordinationschemie seit langem und immer intensiver mit der Reduktion von gebundenem N2 – während die offensichtliche Ladungsübertragung von Metallen in niedriger Oxidationsstufe auf einen Carbonylliganden durch eine Rückbindung kaum als Reduktion angesehen wird. Da in den letzten Jahren viele neue N2-Komplexe mit dem Zentralmetall Eisen beschrieben wurden, schauen wir dort und beim homologen Ruthenium einmal genauer hin.
Ein Blick auf den Grenzorbitalbereich gibt eine Idee, warum N2 kein berauschender Ligand ist:
Valenzorbitale von CO und N2 (mp2/cc-pvtz, isovalue 0.02).
CO ist ein neutraler 2-Elektronen-Donor. Eine Rückbindung wird im Rahmen der IUPAC-Regeln nicht im Sinne einer 2-Elektronen-Reduktion des CO-Liganden interpretiert. Diese Betrachtungsweise ist mit der Behandlung von zum Beispiel Wasserstoff-Liganden nicht ganz konsistent. Bindet die Metallbase [Co(CO)4]− mit einem an Cobalt zentrierten Elektronenpaar ein Proton, so wird das Metallzentrum formal um 2 Elektronen oxidiert, da das Produkt als Hydrido-cobalt(I)-Komplex betrachtet wird – H ist elektronegativer als Co, so dass die beiden Bindungselektronen dem Wasserstoff zugerechnet werden. Anlagerung oder Entfernung eines CO-Liganden ist dagegen für die formale Oxidationsstufe ohne Wirkung, obwohl eine ähnliche Argumentation die Rückbindung dem CO-Liganden zuweisen könnte, der dadurch zum CO2− würde.
Bei N2-Liganden hat es sich eingebürgert, dessen Beladung eingehender zu hinterfragen (wohl deswegen, dass N2-Koordination oft durch dessen Nitrogenase-analoge Reduktion motiviert war). Einen experimenteller Zugang erlauben Diagramme, in denen der Atomabstand in einem zweiatomigen Liganden E2 gegen die E-E-Valenzfrequenz abgetragen wird (der resultierende Verlauf wird als Badgers Regel bezeichnet [Badger's rule]). Figure 4 in [dinitrogen_2010] zeigt ein solches Diagramm, in das als Stützpunkte neben N2 auch N2H2 und N2H4 eingetragen sind. (Wir diskutieren den Unterschied zu Figure 3 in derselben Publikation.)
[dinitrogen_fe_2014]
H. Broda and F. Tuczek:
Katalytische Ammoniaksynthese in homogener Lösung – endlich biomimetisch?
Angew. Chem. 2014, 126, 644–646.
doi:
10.1002/ange.201308780
[dinitrogen_fe_activation_2010]
Y. Lee, N. P. Mankad and J. C. Peters:
Triggering N2 uptake via redox-induced expulsion of coordinated NH3 and N2 silylation at trigonal bipyramidal iron.
Nat. Chem. 2010, 2, 558-565.
doi:
10.1038/nchem.660
[dinitrogen_ru_2010]
T. Kizaki, T. Abe, T. Matsumoto and S. Ogo:
A pH-stable Ruthenium(II)-based Sensing System for Dissolved Dinitrogen.
Chem. Lett. 2010, 39, 128-129.
doi:
10.1246/cl.2010.128
[dinitrogen_review_2010]
J. L. Crossland and D. R. Tyler:
Iron–dinitrogen coordination chemistry: Dinitrogen activation and reactivity.
Coord. Chem. Rev. 2010, 254, 1883–1894.
doi:
10.1016/j.ccr.2010.01.005
[dinitrogen_2010]
P. L. Holland:
Metal-dioxygen and metal-dinitrogen complexes: where are the electrons?
Dalton Trans. 2010, 39, 5415–5425.
doi:
10.1039/C001397H
[dinitrogen_activation2_2010]
N. Hazari:
Homogeneous iron complexes for the conversion of dinitrogen into ammonia and hydrazine.
Chem. Soc. Rev. 2010, 39, 4044–4056.
doi:
10.1039/B919680N
Die für eine starke Rückbindung nicht förderliche Oxidationsstufe +II liegt auch im lange bekannten Nitroprussid-Anion vor. Dessen Natriumsalz, Natrium-pentacyanido-nitrosyl-ferrat(III)-Dihydrat, Na2[Fe(CN)5NO] · 2 H2O, ist ein geläufiges Medikament, das zum Beispiel bei Operationen nach Bedarf infundiert wird um den Blutdruck des Patienten schnell und wirksam zu senken. Nach der Entdeckung der Hormonwirkung von NO wurde erkannt, dass das Ferrat-Ion unter physiologischen Bedingungen NO abspaltet, worauf die Wirkung beruht. NO ist also offensichtlich auch an diesem Eisen(II)-Zentrum weniger fest gebunden als es die Strukturanalyse nahelegt:
Die Strukturparameter des {FeNO}6-Zentrums im Natrium-nitroprussid zeigen wieder ein lineares Fe-N-O-Fragment. Die Fe-N-Bindung ist recht kurz, die gegenüber dem Carbonylferrat deutlich geschwächte Rückbindung zeigt sich jedoch am stark verkürzten N-O-Abstand. Um zu verstehen, dass die Fe-N-Bindung bei weitem nicht so schwach ist wie beim Aqua-nitrosyl-Komplex, ist die low-spin-Konfiguration des Cyanidokomplexes zu beachten. Die sich andeutende Mittelstellung der Fe-N-Bindung – nicht so stabil wie bei einem Eisen(−II)-Zentrum, nicht so schwach wie bei high-spin-Eisen(II) – wird am besten deutlich, wenn eine aufsehenerregende Eigenschaft des Natrium-nitroprussids in die Diskussion einbezogen wird (Hauser, 1977). Beim Bestrahlen von SNP-Kristallen (SNP = sodium nitroprusside) mit grünem Laserlicht bei tiefer Temperatur wird ein metastabiler Zustand (MS2) erhalten, der einer Population von etwa der Hälfte aller Ferrat-Ionen entspricht. Beim Aufwärmen über 165 K geht MS2 in einen weiteren metastabilen Zustand MS1 über. Beide metastabile Zustände haben in der Kälte eine beliebige Lebensdauer. Der Grundzustand kann entweder durch Aufwärmen auf Raumtemperatur oder durch Bestrahlen mit rotem Laserlicht wieder erreicht werden.
Die ungewöhnliche Lebensdauer deutet an, dass es sich bei den metastabilen Zuständen nicht um elektronische Anregungen handelt, sondern dass eine strukturelle Veränderung stattfindet. Diese wurde 1997 erstmals durch Röntgenbeugung nachgewiesen. Aktuelle Rechnungen unterstützen den Befund, dass in MS2 die Nitrosylgruppe eine Art π-Donor-Bindungsmodus einnimmt, der in die Isonitrosyl-Struktur MS1 relaxiert. Im Einklang mit der Arbeitshypothese, dass eine Fe-N-Rückbindung bei Eisen(II)-Zentren nicht nennenswert ist, unterscheiden sich die N-O-Abstände in den drei Formen kaum:
Eine Übersicht zu der an SNP beschriebenen photoinduzierten Bindungsisomerie (engl. photoinduced linkage isomerism) gibt [pli_review_2002]. Wir diskutieren, warum es genau die beiden beobachteten metastabilen Isomere gibt. Hierzu machen wir uns die verschiedenen Komponenten der Fe-NO-Wechselwirkung klar, bei MS2 zum Beispiel die folgenden: